Simultaneous Equations

Here is everything you need to know about simultaneous equations for GCSE maths (Edexcel, AQA and OCR).

You’ll learn what simultaneous equations are and how to solve them algebraically. We will also discuss their relationship to graphs and how they can be solved graphically.

Look out for the simultaneous equations worksheets and exam questions at the end.

What are simultaneous equations?

Simultaneous equations are two or more algebraic equations that share variables such as x and y .

They are called simultaneous equations because the equations are solved at the same time.

The number of variables in simultaneous equations must match the number of equations for it to be solved.

An example of simultaneous equations is
2 x + 4 y = 14
4 x − 4 y = 4

Here are some more:

6a + b = 18

4a + b = 14

3h + 2i = 8

2h + 5i = −2

Each of these equations on their own could have infinite possible solutions.

However when we have at least as many equations as variables we may be able to solve them using methods for solving simultaneous equations.

Representing simultaneous equations graphically

We can consider each equation as a function which, when displayed graphically, may intersect at a specific point. This point of intersection gives the solution to the simultaneous equations.

\[\begin x+y=6\\ -3x+y&=2 \end\]

When we draw the graphs of these two equations, we can see that they intersect at (1,5).

So the solutions to the simultaneous equations in this instance are:

What are simultaneous equations?

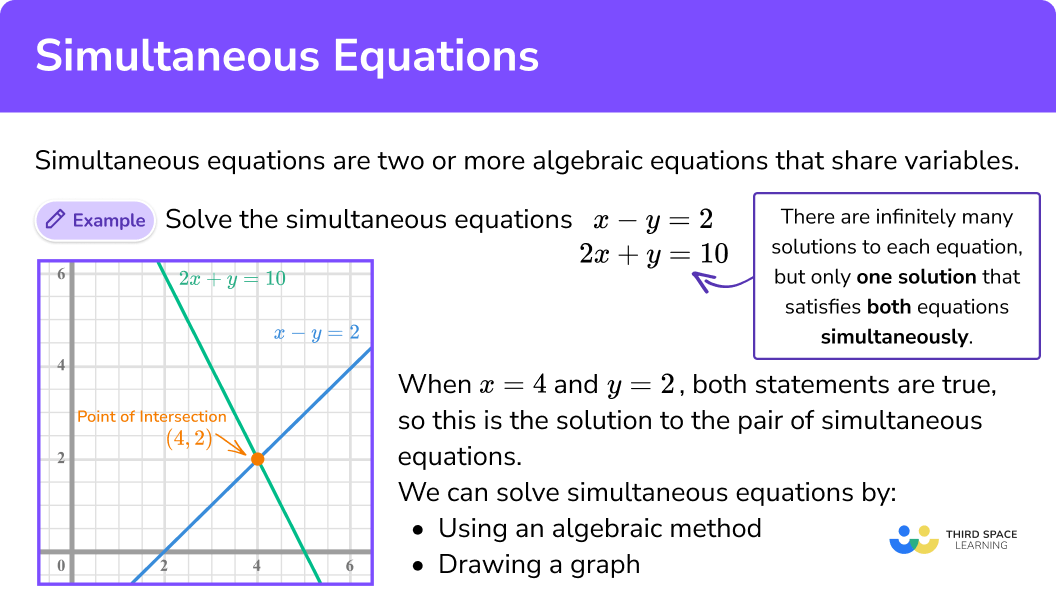
Solving simultaneous equations

When solving simultaneous equations you will need different methods depending on what sort of simultaneous equations you are dealing with.

There are two sorts of simultaneous equations you will need to solve:

linear simultaneous equations
quadratic simultaneous equations

A linear equation contains terms that are raised to a power that is no higher than one.

Linear simultaneous equations are usually solved by what’s called the elimination method (although the substitution method is also an option for you).

Solving simultaneous equations using the elimination method requires you to first eliminate one of the variables, next find the value of one variable, then find the value of the remaining variable via substitution. Examples of this method are given below.

A quadratic equation contains terms that are raised to a power that is no higher than two.

Quadratic simultaneous equations are solved by the substitution method.

What are linear and quadratic simultaneous equations?

Simultaneous equations worksheets

Get your free simultaneous equations worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Simultaneous equations worksheets

Get your free simultaneous equations worksheet of 20+ questions and answers. Includes reasoning and applied questions.

How to solve simultaneous equations

To solve pairs of simultaneous equations you need to:

Use the elimination method to get rid of one of the variables.
Find the value of one variable.
Find the value of the remaining variables using substitution.
Clearly state the final answer.
Check your answer by substituting both values into either of the original equations.

How do you solve pairs of simultaneous equations?

See the examples below for how to solve the simultaneous linear equations using the three most common forms of simultaneous equations.

See also: Substitution

Quadratic simultaneous equations

Quadratic simultaneous equations have two or more equations that share variables that are raised to powers up to 2 e.g. x^ and y^ .

Solving quadratic simultaneous equations algebraically by substitution is covered, with examples, in a separate lesson.

Simultaneous equations examples

For each of the simultaneous equations examples below we have included a graphical representation.

Example 1: Solving simultaneous equations by elimination (addition)

\[\begin 2x+4y&=14\\ 4x-4y&=4 \end\]

Eliminate one of the variables.

By adding the two equations together we can eliminate the variable y .

\[\begin 2x+4y&=14\\ 4x-4y&=4\\ \hline 6x&=18 \end\]

2 Find the value of one variable.

3 Find the value of the remaining variable via substitution.

We know x = 3 so we can substitute this value into either of our original equations.

4 Clearly state the final answer.

\[x=3 \qquad\qquad y=2\]

5 Check your answer by substituting both values into either of the original equations.

\[\begin 4(3)+4(2)&=4\\ 12-8&=4\\ \end\]

This is correct so we can be confident our answer is correct.

Graphical representation of solving by elimination (addition)

When we draw the graphs of these linear equations they produce two straight lines. These two lines intersect at (1,5). So the solution to the simultaneous equations is x = 3 and y = 2 .

Example 2: Solving simultaneous equations by elimination (subtraction)

\[\begin 6 a+b=18 \\ 4 a+b=14 \end\]

Eliminate one of the variables.

By subtracting the two equations we can eliminate the variable b .

\[\begin 6a+b&=18 \\ 4a+b&=14 \\ \hline 2a&=4 \end\]

NOTE: b − b = 0 so b is eliminated

2 Find the value of one variable.

3 Find the value of the remaining variable/s via substitution.

We know a = 2 so we can substitute this value into either of our original equations.

\[\begin 6 a+b &=18 \\ 6(2)+b &=18 \\ 12+b &=18 \\ b &=6 \end\]

4 Clearly state the final answer.

\[a=2 \qquad\qquad b=6\]

5 Check your answer by substituting both values into either of the original equations.

\[\begin 4(2)+(6) &=14 \\ 8+6 &=14 \end\]

This is correct so we can be confident our answer is correct.

Graphical representation of solving by elimination (subtraction)

When graphed these two equations intersect at (1,5). So the solution to the simultaneous equations is a = 2 and b = 6 .

Example 3: Solving simultaneous equations by elimination (different coefficients)

\[\begin 3 h+2 i=8 \\ 2 h+5 i=-2 \end\]

Notice that adding or subtracting the equations does not eliminate either variable (see below).

\[\begin 3 h+2 i=8 \\ 2 h+5 i=-2 \\ \hline 5 h+7 i=6 \end \begin 3 h+2 i&=8 \\ 2 h+5 i&=-2 \\ \hline h-3 i&=10 \end\]

This is because neither of the coefficients of h or i are the same. If you look at the first two examples this was the case.

So our first step in eliminating one of the variables is to make either coefficients of h or i the same.

Eliminate one of the variables.

We are going to equate the variable of h .

Multiply every term in the first equation by 2 .

Multiply every term in the second equation by 3 .

\[\begin 3h+2 i&=8 \\ 2h+5 i&=-2 \\ \\ 6h+4 i&=16 \\ 6h+15 i&=-6 \end\]

Now the coefficients of h are the same in each of these new equations, we can proceed with our steps from the first two examples. In this example, we are going to subtract the equations.

\[\begin 6 h+4 i&=16 \\ 6 h+15 i&=-6 \\ \hline -11 i&=22 \end\]

Note: 6h − 6h = 0 so h is eliminated

Careful: 16 − − 6 = 22

2 Find the value of one variable.

3 Find the value of the remaining variable/s via substitution.

We know i = − 2 so we can substitute this value into either of our original equations.

4 Clearly state the final answer.

\[h=4 \qquad\qquad i=-2\]

5 Check your answer by substituting both values into either of the original equations.

\[\begin 2(4)+5(-2)&=-2 \\ 8-10&=-2 \end\]

This is correct so we can be confident our answer is correct.

Graphical representation of solving by elimination (different coefficients)

When graphed these two equations intersect at (1,5). So the solution to the simultaneous equations is h = 4 and i = − 2 .

Example 4: Worded simultaneous equation

David buys 10 apples and 6 bananas in a shop. They cost £5 in total.
In the same shop, Ellie buys 3 apples and 1 banana. She spends £1.30 in total.
Find the cost of one apple and one banana.

Additional step: conversion

We need to convert this worded example into mathematical language. We can do this by representing apples with a and bananas with b .

\[\begin 10a+6b&=5 \\ 3a+1b&=1.30 \end\]

Notice we now have equations where we do not have equal coefficients (see example 3).

Eliminate one of the variables.

We are going to equate the variable of b .

Multiply every term in the first equation by 1 .

Multiply every term in the second equation by 6 .

\[\begin 10 a+6 b&=5 \\ 3 a+1 b&=1.30 \\ \\ 10 a+6 b&=5 \\ 18 a+6 b&=7.80 \end\]

Now the coefficients of b are the same in each equation we can proceed with our steps from the previous examples. In this example, we are going to subtract the equations.

\[\begin 10a+6b &=5 \\ 18a+6b &=7.80 \\ \hline -8a &=-2.80 \end\]

NOTE: 6b − 6b = 0 so b is eliminated

2 Find the value of one variable.

Note: we ÷ (− 8) not 8

3 Find the value of the remaining variable/s via substitution.

We know a = 0.35 so we can substitute this value into either of our original equations.

4 Clearly state the final answer.

\[a=0.35 \qquad\qquad b=0.25\]

1 apple costs £0.35 (or 35p ) and 1 banana costs £0.25 (or 25p ).

5 Check your answer by substituting both values into either of the original equations.

\[\begin 3(0.35)+1(0.25) & =1.30 \\ 1.05+0.25 & =1.30 \end\]

This is correct so we can be confident our answer is correct.

Graphical representation of the worded simultaneous equatio

When graphed these two equations intersect at (1,5). So the solution to the simultaneous equations is a = 0.35 and b = 0.25 .

Common misconceptions

Incorrectly eliminating a variable.
Using addition to eliminate one variable when you should subtract (and vice-versa).

Step by step guide: Negative numbers (coming soon)

Practice simultaneous equations questions

1. Solve the Simultaneous Equation

6x +3y = 48
6x +y =26